The Mathematical Mechanics of the Pleasing Proportions

nnn

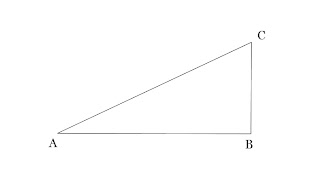
n Most people will remember pin(π) from their schooldays, as in πr², which is the ratio of thenradius to the circumference of a circle. Pi can be variously calculatedn– a rough approximation is the fraction 22/7, a slightly more accurate form isn3.142. Another ratio, perhaps not as well known, is phi (φ), which isnthe ratio of one quantity to another, wherein the ratio of the first quantitynto the second is in the same ratio as the first quantity to the whole. This cannbest be seen in this diagram, where a is to b as a+b is tona.

nAlgebraically, this is (1+√5)/2, which gives a rough value of 1.618.nThis proportion has been given a number of names in addition to phi; itnhas also been called the Golden Mean, the Golden Ratio, the Golden Section ornthe Divine Proportion.

nYou can easily construct your own Golden Section with anruler and a pair of compasses.

nTake a line of length AB.

nDraw a vertical linenat B equal to half of AB, forming a line BC, then join A to C to produce anright-angled triangle.

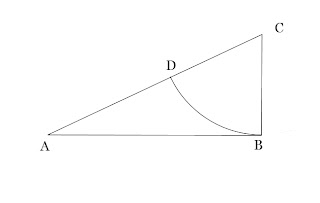
nWith your compasses, draw an arc from centre C with anradius CB, from B to cross AC at point D.

nRe-set the compasses to radius AD,nand from centre A draw another arc from D to cross AB at point E.

nThenproportion of AE:EB is the same as AE:AB – the Golden Section or φ.

nConversely,nto increase a line by φ, take your line AB.

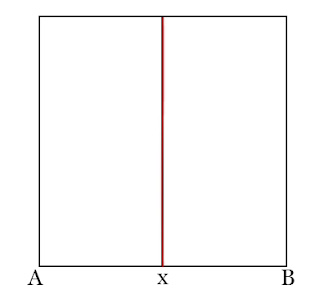
nForm a rectangle above AB andndivide this rectangle into two exact halves, with a point x halfway between Anand B.

n
n

nDraw a diagonal line from x to the top right angle above B, giving y.

nSet the compasses with a radius xy and with centre x draw an arc from y toncross the extension of AB at point z.

nThat gives you the Golden Section again.

n(On the other hand, you could just measure thenline and multiply it by 1.618, adding the product to the end of your originalnline).

nThe Golden Ratio is not just ofninterest to mathematicians; artists, architects, biologists, historians,nmusicians, psychologists and proponents of just about any other discipline havenfound phi to be of interest. In the arts, phi is particularlyninteresting because it is so aesthetically pleasing to the human eye. In 1509,nthe Franciscan friar Luca Pacioli published his three-volume De DivinanProportione in which he explored aspects of the Divine Proportion, togethernwith Vitruvian proportions, and with illustrations by Leonardo da Vinci,nPacioli’s works were enormously influential on Renaissance and later art; thenGolden Section continues to be used by artists and designers to this day.nHowever, because the ratio is so satisfying to the eye, many people discover itnwhere it was not deliberately employed, a case in point being the Parthenon ofnancient Greece.

nThere is no evidence that the Greeks were aware of phinwhen the Parthenon was built (begun 447 BCE, completed 438 BCE), and Euclid, innhis Elements (308 BCE) merely discusses it as an interesting irrationalnnumber – the ancients, notably Vitruvius, were more interested in the ratios ofnwhole numbers. This hasn’t stopped people overlaying phi on thenParthenon and finding instances of it, but this is a highly selectivenprocedure, conveniently ignoring instances where phi doesn’t occur. Thenbuilders of the Parthenon built to pleasing proportions, certainly, but it wasnmore like the photographer’s Rule of Thirds, where the subject of a picture isnplaced off-centre, at about a third of the frame, to give a more interestingnshot. It just so happens that phi is also very roughly at about a third,nwhich causes some to see it where it hasn’t actually been used.

nIt’s not unlikenthings like leys, the supposed lines linking ancient ‘holy’ sites. It’s fun tonget a map and a ruler and make your own – I’ve seen lines that perfectly alignnpetrol stations, branches of Woolworths or telephone boxes across the landscapen– showing that if you look hard enough, you’ll eventually discover whatever itnwas you set out find.